目录
1.冒泡排序
2.插入排序
3.选择排序
4.希尔排序
5.快速排序
6.简单选择排序
7.堆排序
8.归并排序
基数排序
外部排序
置换-选择排序
最佳归并树
合并两个有序单向链表
序列化和反序列化二叉树
单向链表反转
判断链表是否有环
解题思路:
用两个栈实现队列
二分查找有序数组
二叉树的层次遍历:
排序:按照关键字的大小进行递增/递减排序
排序算法的评价指标:
稳定性(关键字相同的元素经过排序后相对顺序是否会改变)
时间/空间复杂度
排序的分类:
1.内部排序(数据都在内存中)
2.外部排序(数据太多,无法全部放入内存)1.冒泡排序
package demo.sort;
/**
* @author pert
* @date 2021年08月07日 21:56
*/
public class sort {
// 冒泡排序
//这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
// 冒泡排序算法的运作如下:
// 比较相邻的元素。如果第一个比第二个大,就交换他们两个。
// 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。在这一点,最后的元素应该会是最大的数!!!
// 持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
public static void main(String[] args) {
int arr[]={32,4,101,5,67,34,78,45,1,7,34};
int tmp= -1;
for (int i = 0; i < arr.length; i++) {
// 每次循环把最大数放在最下面:
for (int j = 1; j < arr.length-i; j++) {
if(arr[j]<arr[j-1]){
tmp=arr[j-1];
arr[j-1]=arr[j];
arr[j]=tmp;
}
}
System.out.print("第"+i+"次:");
for (int k = 0; k < arr.length; k++) {
System.out.print(arr[k]+"\t");
}
System.out.println(" ");
}
System.out.print("最后结果:");
for (int k = 0; k < arr.length; k++) {
System.out.print(arr[k]+"\t");
}
}
}package demo.sort;
/**
* @author pert
* 1.冒泡排序
* BubbleSort
* @date 2021年08月07日 21:56
*/
public class sort1 {
public static int[] BubbleSort(int arr[]){
//考虑其他情况:
if (arr == null || arr.length == 0 ) {
return null;
} else if(arr.length==1){
return arr;
}
int tmp= -1;
for (int i = 0; i < arr.length; i++) {
// 每次循环把最大数放在最下面:
for (int j = 1; j < arr.length-i; j++) {
if(arr[j]<arr[j-1]){
tmp=arr[j-1];
arr[j-1]=arr[j];
arr[j]=tmp;
}
}
}
return arr;
}
public static void main(String[] args) {
int arr[]={32,4,101,5,67,34,78,45,1,7,34};
int []sort1=BubbleSort(arr);
System.out.print("最后结果:");
for (int k = 0; k < arr.length; k++) {
System.out.print(sort1[k]+"\t");
}
}
}
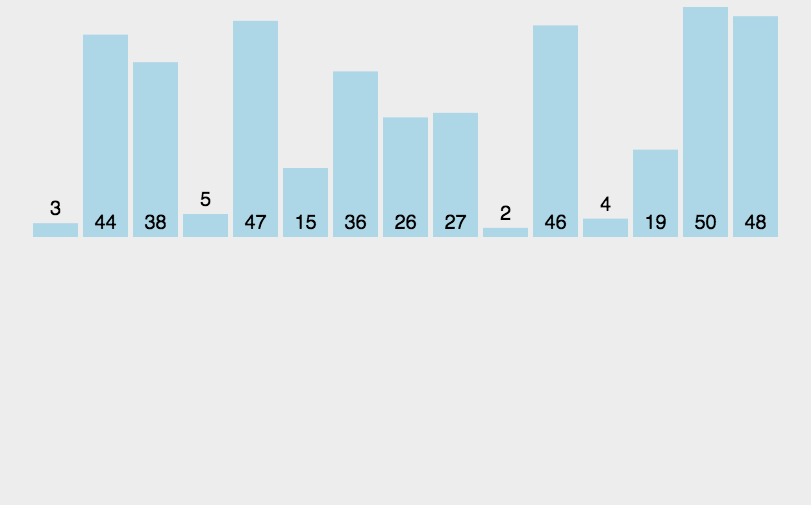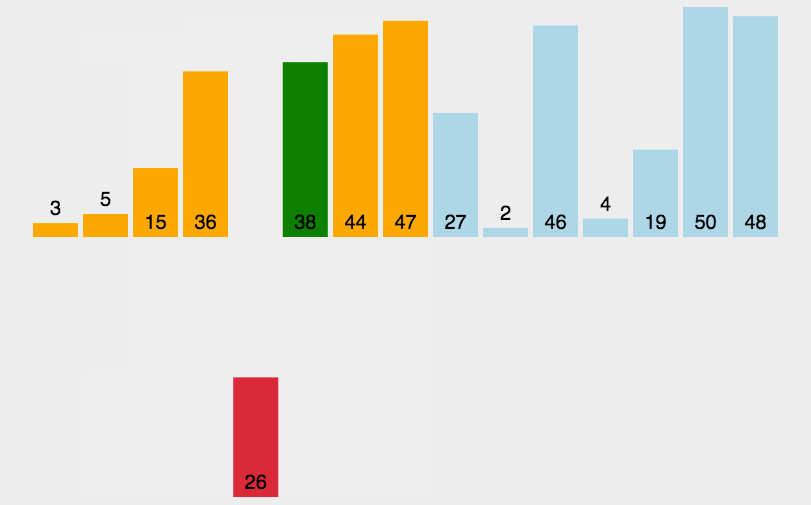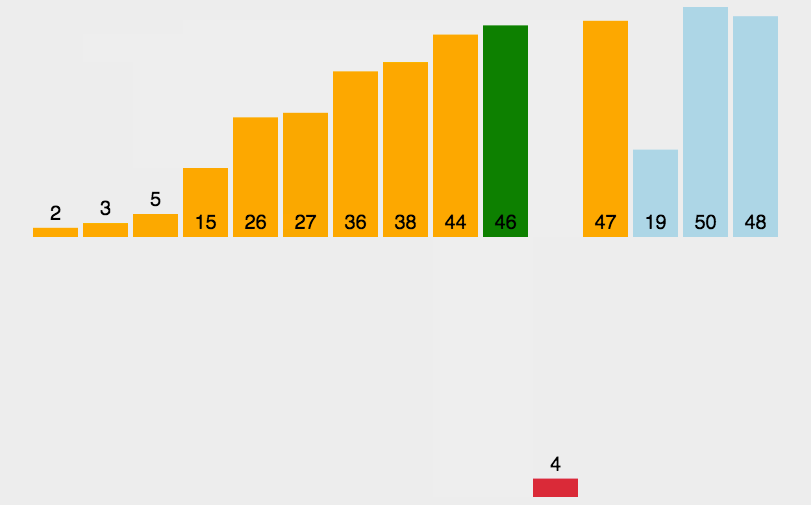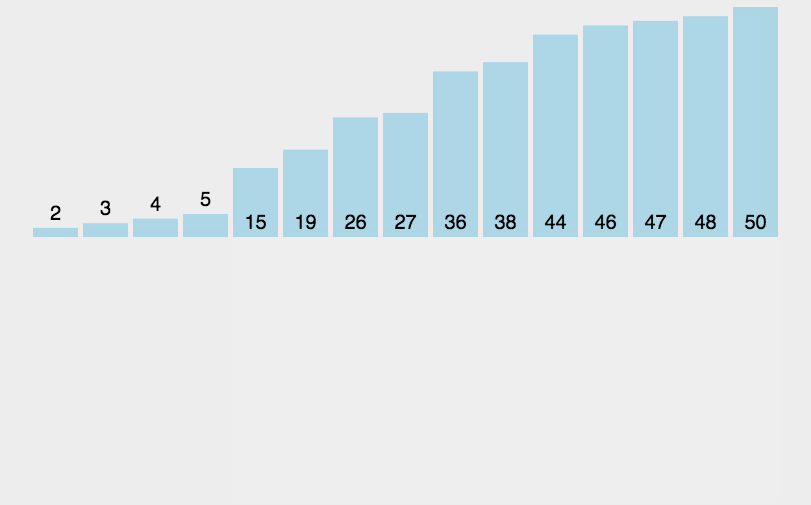
2.插入排序
package demo.sort;
/**
* @author pert
* 2.插入排序
* @date 2021年08月07日 21:56
*/
public class sort2 {
//2.插入排序工作原理
// 通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
// 在从后向前扫描过程中,需要反复把已排序元素逐步向后挪位,为最新元素提供插入空间!!!
// 最佳情况:T(n) = O(n) 最坏情况:T(n) = O(n2) 平均情况:T(n) = O(n2)
public static void main(String[] args) {
int arr[]={32,4,101,5,67,34,78,45,1,7,34};
int current;
int len=arr.length;
int preIdx;
if(arr==null||arr.length==0){
System.out.println("数组为空!");
return;
}else if(len==1){
System.out.println(arr[0]);
return;
}
// for (int i = 0; i < len; i++) Exception in thread "main" java.lang.ArrayIndexOutOfBoundsException: 11
// 9个数表8次=========length个数比较length-1次
for (int i = 0; i < len-1; i++) {
current= arr[i+1];
// 前一个数的下标:
preIdx = i;
// 拿当前的数与之前已排序序列逐一往前比较,
// 如果比较的数据比当前的大,就把该数往后挪一步
while(preIdx >=0 && arr[preIdx]>current ){
//注意&&条件执行的先后顺序;若 while(arr[preIdx]>current && preIdx >=0),若preIdx先=-1,但会先判断arr[preIdx]>current,就会报数组索引越界异常ArrayIndexOutOfBoundsException
// 移位:
arr[preIdx+1]=arr[preIdx];
preIdx--;
}
arr[preIdx+1]=current;
}
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i]+"\t");
}
}
}package demo.sort;
/**
* @author pert
* 2.插入排序
* @date 2021年08月07日 21:56
*/
public class sort2 {
public static int[] charupaixu(int []arr){
int current;
int len=arr.length;
int preIdx;
if(arr==null||arr.length==0){
System.out.println("数组为空!");
return arr;
}else if(len==1){
return arr;
}
for (int i = 0; i < len-1; i++) {
current= arr[i+1];
preIdx = i;
while(preIdx >=0 && arr[preIdx]>current ){
arr[preIdx+1]=arr[preIdx];
preIdx--;
}
arr[preIdx+1]=current;
}
return arr;
}
public static void main(String[] args) {
int arr[]={32,4,101,5,67,34,78,45,1,7,34};
int sort3[]=charupaixu(arr);
for (int i = 0; i < sort3.length; i++) {
System.out.print(sort3[i]+"\t");
}
}
}
3.选择排序
package demo.sort;
/**
* @author pert
* 2.选择排序 不需要额外存储空间,重复选择做小元素
* @date 2021年08月07日 21:56
*/
public class sort33 {
public static void main(String[] args) {
int arr[] = {32, 4, 101, 5, 67, 34, 78, 45, 1, 7, 34,2};
for (int i = 0; i < arr.length-1; i++) {
// 标记第i各元素为最小值
int min=i;
// 找到最小元素的角标:
for (int j = i+1; j < arr.length; j++) {
if(arr[j]<arr[min])
min=j;
}
// 以下放到外层!!!!!!!!!!
if(i != min){
int temp=arr[i];
arr[i]=arr[min];
// 第i位置插入第i小的值:
arr[min]=temp;
}
}
for (int k:arr) {
System.out.print(k+"\t");
}
}
}4.希尔排序

package demo.sort;
/**
* @author pert
* 希尔排序 ShellSort 步长对半分的插入排序
* @date 2021年08月08日 11:43
*/
public class sort3 {
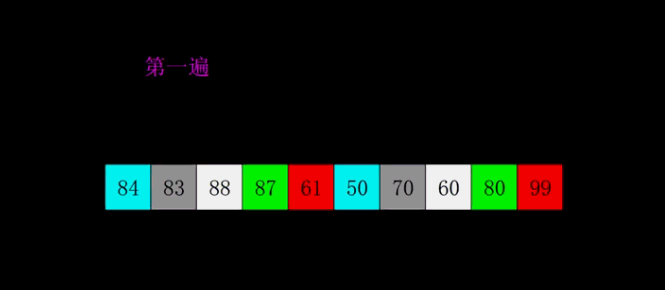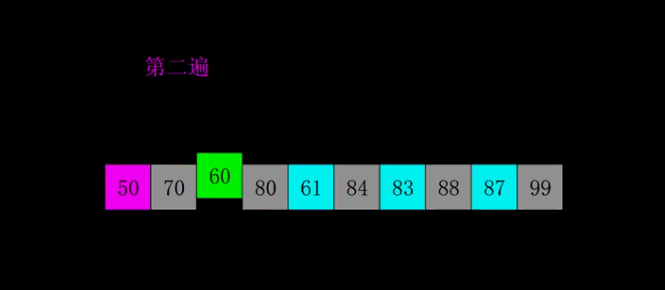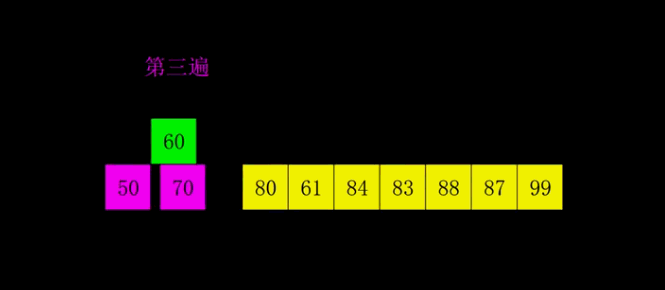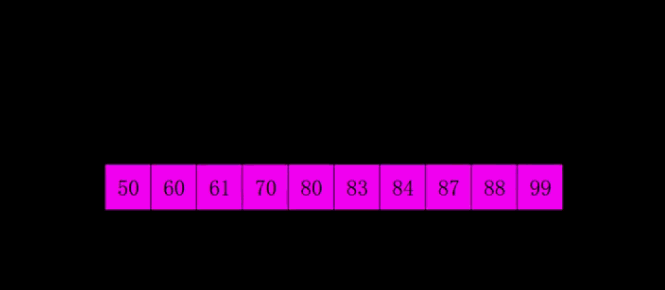
// 希尔排序(Shell’s Sort)是插入排序的一种,是直接插入排序算法的一种更高版本的改进版本。
//
// 把记录按步长gap分组,对每组记录采用直接插入排序方法进行排序;
// 随着 步长逐渐减小, 所分成的组包含的记录越来越多;
// 当步长值减小到1时,整个数据合成一组,构成一组有序记录,完成排序;
//步长对半分:
public static void main(String[] args) {
int arr[]={32,4,101,5,67,34,78,45,1,7,34};
// 设置步长
for (int step=arr.length/2;step>0;step/=2) {
//对一个步长区间进行比较 [step,arr.length)
// i从中到后
for (int i=step; i<arr.length; i++) {
int value=arr[i];
int j;
//对步长区间中具体的元素进行比较
// j从0开始;依次减少步长单位
for (j=i-step;j>=0&&arr[j]>value;j=j-step){
//j为左区间的取值,j+step为右区间与左区间的对应值。
arr[j+step]=arr[j];
}
//此时step为一个负数,[j + step]为左区间上的初始交换值
arr[j+step]=value;
}
}
}
}package demo.sort;
/**
* @author pert
* 希尔排序 ShellSort
* @date 2021年08月08日 11:43
*/
public class sort3fengzhuang {
public static void main(String[] args) {
int arr[]={32,4,101,5,67,34,78,45,1,7,34};
shellSort(arr);
for (int i : arr) {
System.out.print(i + "\t");
}
}
private static void shellSort(int[] arr) {
//step:步长
for (int step = arr.length / 2; step > 0; step /= 2) {
//对一个步长区间进行比较 [step,arr.length)
for (int i = step; i < arr.length; i++) {
int value = arr[i];
int j;
//对步长区间中具体的元素进行比较
for (j = i - step; j >= 0 && arr[j] > value; j -= step) {
//j为左区间的取值,j+step为右区间与左区间的对应值。
arr[j + step] = arr[j];
}
//此时step为一个负数,[j + step]为左区间上的初始交换值
arr[j + step] = value;
}
}
}
}5.快速排序
package demo.sort;
/**
* @author pert
* 还要再消化!!!!!!!!!!!sort(int[] array, int left, int right)
* 快速排序 quickSort 分治算法的一种实例:划分+分而治之
* 1.划分:将一个数组A[low,.....hight]划分为N组数组A[low...q]、A[q+1,...high];使得A[low...q]中每个元素都小于或等于A[q+1,...high]中的元素
* 2.分而治之:对两个子数组A[low...q]、A[q+1,...high]递归调用快速排序
* 快速排序之所以比较快,是因为相比冒泡排序,每次的交换都是跳跃式的,每次设置一个基准值,将小于基准值的都交换到左边,大于基准值的都交换到右边,
* 这样不会像冒泡一样每次都只交换相邻的两个数,因此比较和交换的此数都变少了,速度自然更高。
* @date 2021年08月08日 14:06
*/
public class sort5 {
// 利用分治法来对待排序序列进行分治排序,它的思想主要是通过一趟排序将待排记录分隔成--------------独立的两部分,
// 其中的一部分比关键字小,后面一部分比关键字大,然后再对这前后的两部分分别采用这种方式进行排序,通过递归的运算最终达到整个序列有序
public static void quickSort(int[] array) {
int len;
if(array == null || (len = array.length) == 0 || len == 1) {
return ;
}
sort(array, 0, len - 1);
}
/**
* 快排核心算法,递归实现
* @param array
* @param left
* @param right
*/
public static void sort(int[] array, int left, int right) {
if(left > right) {
return;
}
// base中存放基准数
int base = array[left];
int i = left, j = right;
while(i != j) {
// 顺序很重要,先从右边开始往左找,直到找到比base值小的数
while(array[j] >= base && i < j) {
j--;
}
// 再从左往右边找,直到找到比base值大的数
while(array[i] <= base && i < j) {
i++;
}
// 上面的循环结束表示找到了位置或者(i>=j)了,交换两个数在数组中的位置
if(i < j) {
int tmp = array[i];
array[i] = array[j];
array[j] = tmp;
}
}
// 将基准数放到中间的位置(基准数归位)
array[left] = array[i];
array[i] = base;
// 递归,继续向基准的左右两边执行和上面同样的操作
// i的索引处为上面已确定好的基准值的位置,无需再处理
sort(array, left, i - 1);
sort(array, i + 1, right);
}
public static void main(String[] args) {
int arr[] = {0,32, 4, 101, 5, 67, 34, 78, 45, 1, 7, 34,2};
quickSort(arr);
for(int k :arr){
System.out.print(k+"\t");
}
}
}6.简单选择排序
package demo.sort;
/**
* @author pert
* 简单选择排序实现
* 和选择排序一样 不需要额外存储空间,重复选择做小元素
* 通过n-i次关键字之间的比较,从n-i+1个记录中选出关键字最小的记录,并和第i (1 ≤ i ≤ n)个记录交换。
* 简单选择排序的性能要略优于冒泡排序
* @date 2021年08月08日 15:12
*/
public class sort6 {
//置换
public static void swap(int[] elem, int i, int j) {
int temp = elem[i];
elem[i] = elem[j];
elem[j] = temp;
}
//简单选择排序
public static void selectSort(int[] elem) {
int min;
for (int i = 0; i < elem.length; i++) {
min = i;
for (int j = i+1; j < elem.length; j++) {
if(elem[min] > elem[j]) {
min = j;
}
}
if(min != i) {
swap(elem, i, min);
}
}
}
public static void main(String[] args) {
int arr[] = {32, 4, 101, 5, 67, 34, 78, 45, 1, 7, 34,2};
selectSort(arr);
for (int i :arr) {
System.out.print(i + "\t");
}
}
}7.堆排序






package demo.sort;
import static demo.sort.sort72.HeapSort;
/**
* @author pert
* 堆排序(Heap Sort)是指利用堆这种数据结构所设计的一种排序算法。
* @date 2021年08月08日 15:12
*/
public class sort72 {
//建立大根堆:
static void BuildMaxHeap(int A[],int len){
for (int i = len/2; i >0; i--) {
HeadAdjust(A,i,len);
}
}
// 将以k为根的子树调整为大根堆
static void HeadAdjust(int A[],int k,int len){
A[0]=A[k]; //A[0]暂存子树的根节点
for (int i = 2*k; i <=len ; i*=2) { //沿key较大的子节点向下筛选 i <=len
if(i<len && A[i]<A[i+1])
i++; //取key较大的子节点的下标
if(A[0]>=A[i]) break; //筛选结束
else{
A[k]=A[i]; //将A[i]调整到双亲节点上
k=i; //修改k值,以便继续向下筛选
}
}
A[k]=A[0];
}
//堆排序的完整逻辑:
static void HeapSort(int A[],int len){
BuildMaxHeap(A,len); //初始建堆
for (int i = len; i >1 ; i--) { //n-1趟的交换和建堆过程
// swap(A[i],A[1]); //堆顶和堆底元素交换
// System.out.println(A[i-1]);
int tmp=A[i];
A[i]=A[1];
A[1]=tmp;
HeadAdjust(A,1,i-1); //把剩余的待排序的元素整理成堆
}
}
public static void main(String[] args) {
//数组从1开始,第0个用来存放临时根节点
int arr[] = { 0,1,6,8, 4, 101, 5, 67, 34, 78, 45, 7, 34,2,8,9};
HeapSort(arr,arr.length-1);
for (int i = 1; i < arr.length; i++) {
System.out.print(arr[i] + "\t");
}
}
}8.归并排序







package demo.sort;
/**
* @author pert
* 归并排序:是分治的一个实例,适用于链表排序,是稳定的算法
* 归并:把两个已排序文件合并成一个更大的已排序文件的过程
* 将待排序元素分成大小大致相同的2个子集合,分别对2个子集合进行排序,最终将排好序的子集合合并成为所要求的排好序的集合。
* 参考:
* @date 2021年08月08日 15:45
*/
public class sort8 {
public static void main(String[] args) {
int arr[] = {32, 4, 101, 5, 67, 34, 78, 45, 1, 7, 34,2};
int[] tmp = new int[arr.length]; //新建一个临时数组存放
mergeSort(arr,0,arr.length-1,tmp);
for(int i:arr){
System.out.print(i+"\t");
}
}
public static void merge(int[] arr,int low,int mid,int high,int[] tmp){
int i = 0;
int j = low,k = mid+1; //左边序列和右边序列起始索引
// tmp[]从排序大小的两段数组依次从小插入 (二路归并)
while(j <= mid && k <= high){
if(arr[j] < arr[k]){
tmp[i++] = arr[j++];
}else{
tmp[i++] = arr[k++];
}
}
//若左边或者右边序列还有剩余,则将其全部拷贝进tmp[]中
while(j <= mid){
tmp[i++] = arr[j++];
}
while(k <= high){
tmp[i++] = arr[k++];
}
// 将tmp的值装入原来的arr[]对应位置:
for(int t=0;t<i;t++){
arr[low+t] = tmp[t];
}
}
public static void merge2(int[] arr,int low,int mid,int high,int[] tmp){
int i,j,k;
// 将arr中所有元素复制到tmp中
for ( k = low; k <= high; k++)
tmp[k]=arr[k];
// 归并: k为arr的索引指针;i,j为tmp的前、中指针
for (i =low, j=mid+1, k=i; i <= mid&&j<=high ; k++) {
if(tmp[i]<=tmp[j])
arr[k]=tmp[i++];
else
arr[k]=tmp[j++];
}
// 剩余的装入arr尾部:
while (i<=mid) arr[k++]=tmp[i++];
while (j<high) arr[k++]=tmp[j++];
}
public static void mergeSort(int[] arr,int low,int high,int[] tmp){
if(low<high){
int mid = (low+high)/2;
mergeSort(arr,low,mid,tmp); //对左边序列进行归并排序
mergeSort(arr,mid+1,high,tmp); //对右边序列进行归并排序
// merge(arr,low,mid,high,tmp); //合并两个有序序列
merge2(arr,low,mid,high,tmp);
}
}
}基数排序
外部排序
置换-选择排序
最佳归并树
合并两个有序单向链表
/*输入:
1 2 3 4 5
2 3 4 5 6
输出:
1 2 2 3 3 4 4 5 5 6*/public class Link {
int data;
Link next;
public Link(){
}
public Link(int data){
this.data=data;
}
}
package com.pert.summer.test;
/**
* @author pert
* @date 2021年08月20日 15:15
*/
public class 合并链表 {
/*递归方式合并两个单链表*/
public static Link mergeTwoList(Link node1,Link node2){
if(node1==null&&node2==null){
return null;
}
if(node1==null||node2==null){
return node1!=null?node1:node2;
}
// merge到head上:
Link head=null;
if(node1.data<node2.data){
head=node1;
head.next=mergeTwoList(node1.next,node2);
}else {
head=node2;
head.next=mergeTwoList(node1,node2.next);
}
return head;
}
public static void main(String[] args) {
Link node1=new Link(1);
Link node2=new Link(2);
Link node3=new Link(3);
Link node4=new Link(4);
Link node5=new Link(5);
node1.next=node2;
node2.next=node3;
node3.next=node4;
node4.next=node5;
Link nodea=new Link(1);
Link nodeb=new Link(2);
Link nodec=new Link(3);
Link noded=new Link(4);
Link nodee=new Link(5);
nodea.next=nodeb;
nodeb.next=nodec;
nodec.next=noded;
noded.next=nodee;
Link a=mergeTwoList(node1,nodea);
while(a!=null){
System.out.print(a.data+"\t");
a=a.next;
}
}
}序列化和反序列化二叉树
public class TreeNode {
int val = 0;
TreeNode left = null;
TreeNode right = null;
public TreeNode(int val) {
this.val = val;
}
}
//序列化和反序列化二叉树:将一棵树遍历、加载进字符串中
public class 序列化和反序列化二叉树 {
public static int index = -1;
String Serialize(TreeNode root) {
StringBuilder s=new StringBuilder();
if(root==null){
s.append("#,");
return s.toString();
}
s.append(root.val+",");
s.append(Serialize(root.left));
s.append(Serialize(root.right));
return s.toString();
}
// str:为序列化后的字符串
static TreeNode Deserialize(String str) {
index++;
int len=str.length();
if(index>=len){
return null;
}
String[]DLRseq=str.split(",");
TreeNode leave=null;
if(!DLRseq[index].equals("#")){
leave=new TreeNode(Integer.valueOf(DLRseq[index]));
leave.left=Deserialize(str);
leave.right=Deserialize(str);
}
return leave;
}
public static void main(String[] args) {
String a="1,32,5,65,7,32";
TreeNode leavel1=Deserialize(a);
System.out.println(leavel1);
}
}通过栈 反转链表
import java.util.Stack;
public class Solution {
public ListNode ReverseList(ListNode head) {
Stack<ListNode> stack= new Stack<>();
//把链表节点全部摘掉放到栈中
while (head != null) {
stack.push(head);
head = head.next;
}
if (stack.isEmpty())
return null;
ListNode node = stack.pop();
ListNode dummy = node;
//栈中的结点全部出栈,然后重新连成一个新的链表
while (!stack.isEmpty()) {
ListNode tempNode = stack.pop();
node.next = tempNode;
node = node.next;
}
//最后一个结点就是反转前的头结点,一定要让他的next
//等于空,否则会构成环
node.next = null;
return dummy;
}
}单向链表反转
public class ListNode {
public ListNode next;//指针、引用
public int val;
public ListNode(){}
public ListNode(int val){
this.val=val;
}
}
public class 链表反转 {
// 这个的思路就是 俩个指针,把一个链表分成俩个部分, newNode是已经反转部分, curNode是为反转部分,然后通过俩个指针的配合,不断的右移直到前部反转
// 借助一个
public ListNode reverserList(ListNode head){
if(head==null){
return null;
}
// 当前节点,上一个节点,下一个节点
// 定义一个游标,当前指向哪里
ListNode currNode=head;
// 存上一个节点
ListNode preNode=null;
while (currNode!=null){
//最关键的就是暂存一下当前节点的下一个节点
ListNode nextNode=currNode.next;//暂存
currNode.next=preNode;
// 为下一次做准备:
preNode=currNode;
currNode=nextNode;
}
return preNode;
}
public static void main(String[] args) {
}
}判断链表是否有环
解题思路:
我们遍历链表中的每个节点,并将它记录下来;一旦遇到了此前遍历过的节点,就可以判定链表中存在环。借助哈希表可以很方便地实现
1、遍历链表,并将访问过的结点存储到哈希表中
2、判断结点是否在哈希表中,若存在则返回 true
3、遍历结束,则返回 false
ADT:
class ListNode {
int val;
ListNode next;
ListNode(int x) {
val = x;
next = null;
}
}
public class 判断链表中是否有环 {
public boolean hasCycle(ListNode head) {
ListNode pos = head;
// 哈希表记录访问过的结点
Set<ListNode> visited = new HashSet<ListNode>();
while (pos != null) {
// 判断结点是否被访问
if (visited.contains(pos)) {
return true;
} else {
// 结点记录添加到哈希表中
visited.add(pos);
}
// 遍历
pos = pos.next;
}
return false;
}
}
方法二:声明两个指针,一个指针走一次经过两个节点(快指针quick),另一个走一次经过一个节点(慢指针slow)
方法说明:快指针走的比较快,若链表有环,则一定会追上慢指针,若无环,则会走到链表末端。
public class Solution {
public boolean hasCycle(ListNode head) {
==//声明两个节点从头开始遍历节点==
ListNode quick = head;
ListNode slow = head;
//当快指针能够走到头表示无环
while(quick!=null&&quick.next!=null){
quick = quick.next.next;
slow = slow.next;
if(quick==slow){
return true;
}
}
return false;
}
}
方法一:循环遍历节点,遍历一个便标记一个,遍历过程判断是否被标记,若已被标记则表示有环
方法说明:头指针移动,若到达之前到达过的位置则表示有环,若无环则会走到链表末端。
public class Solution {
public boolean hasCycle(ListNode head) {
//声明一个set存放已遍历的节点,即为标记节点(Set中不允许重复元素)
Set<ListNode> set = new HashSet<>();
while(head!=null) {
if(set.contains(head)) {
return true;
}else {
set.add(head);
head = head.next;
}
}
return false;
}
}用两个栈实现队列
第一个栈如对操作,第二个栈出队操作,栈2为空时,压入栈1的所有元素
/**
* @author pert
* 当插入时,直接插入 stack1
* 当弹出时,当 stack2 不为空,弹出 stack2 栈顶元素,如果 stack2 为空,将 stack1 中的全部数逐个出栈入栈 stack2,再弹出 stack2 栈顶元素
* @date 2021年08月20日 20:44
*/
public class 用两个栈实现队列 {
Stack<Integer> stack1 = new Stack<Integer>();
Stack<Integer> stack2 = new Stack<Integer>();
public void push(int node) {//入栈
stack1.push(node);
}
public int pop() {//出栈
if(stack2.size()==0){
for (int i=0;i<=stack1.size();i++){
// while (stack1.size()!=0){
stack2.push(stack1.pop());
}
}
return stack2.pop();
}
}二分查找有序数组
public class 二分查找 {
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
* 如果目标值存在返回下标,否则返回 -1
* @param nums int整型一维数组
* @param target int整型
* @return int整型
*/
public static int search (int[] nums, int target) {
// write code here
int left = 0, right = nums.length - 1;
int idx = -1;
while (left <= right) {
// int mid=(left + right)/2;
int mid = (left + right) >> 1;
if (nums[mid] == target) {
idx = mid;
right = mid - 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else {
left = mid + 1;
}
}
return idx;
}
public static void main(String[] args) {
int a[]={1,2,2,5,5,7,9,11,23,43,45,67,78,786};
int aim=search(a,5);
System.out.println("排序:"+aim);
}
}二叉树的层次遍历:
public class 求二叉树的层序遍历 {
/**
*
* @param root TreeNode类
* @return int整型ArrayList<ArrayList<>>
* 如何确定换行?
* 标识出 当前层和下一层的分界位置
* 将队列中的值按层一次一次遍历;即:一次性将当前队列中的当前层的元素遍历完,再在一次性遍历下一层队列元素;
*/
public ArrayList<ArrayList<Integer>> levelOrder(TreeNode root) {
ArrayList<ArrayList<Integer>> result = new ArrayList<>();
Queue<TreeNode> queue = new LinkedList<>();
if (root != null) {
queue.offer(root);
while (!queue.isEmpty()) {
ArrayList<Integer> levelList = new ArrayList<>();//叶子集合
int length = queue.size(); // - 区分:标识当前层和下一层的分界位置 根据节点大小区分节点所在层数
for (int i = 0; i < length; i++) {
TreeNode curr = queue.poll();
if (curr.left != null) {
queue.offer(curr.left);
}
if (curr.right != null) {
queue.offer(curr.right);
}
levelList.add(curr.val);
}
if (!levelList.isEmpty()) {
result.add(levelList);
}
}
}
return result;
}
}方法二:
//4.层序遍历,这个是最符合常规思维的遍历方式,从上往下,一层一层的从左往右遍历,此处结果为1-2-3-4-5-6-7-8-9
//层序遍历(一层一层的遍历)
public static void LaywerTraverse(TreeNode node){
if(node == null)
return;
// 初始化一个链表节点队列:
LinkedList<TreeNode> mList = new LinkedList<>();
mList.add(node);
TreeNode currentNode;//currentNode只有data和左右指针
while (!mList.isEmpty()){
currentNode = mList.poll();//队首元素出队;先进先出
// poll是队列数据结构实现类的方法,从队首获取元素,同时获取的这个元素将从原队列删除;
// pop是栈结构的实现类的方法,表示返回栈顶的元素,同时该元素从栈中删除,当栈中没有元素时,调用该方法会发生异常
System.out.println(currentNode.key);
if(currentNode.left != null){
mList.add(currentNode.left);
}
if(currentNode.right != null){
mList.add(currentNode.right);
}
}